Linear Regression With One Variable

Linear Regression with one variable is a statistical method used for predicting the relationship between a dependent variable and a single independent variable. It assumes a linear relationship, aiming to find the best-fit line that minimizes the sum of squared differences between actual and predicted values.

Libraries Required

import numpy as np
import matplotlib.pyplot as plt
import math

Some Plotting Fxn

def plt_house_x(X, y, f_wb=None, ax=None):
    ax.scatter(X, y, marker='x', c='r', label="Actual Value")
    ax.set_ylabel("Y-data")
    ax.set_xlabel("X-data")
    ax.plot(X, f_wb, label="Our Prediction")
    ax.legend()


def mk_cost_lines(x, y, w, b, ax):
    label = 'Cost of point'
    addedbreak = False
    for p in zip(x, y):
        f_wb_p = w*p[0]+b
        c_p = ((f_wb_p - p[1])**2)/2
        c_p_txt = c_p
        ax.vlines(p[0], p[1], f_wb_p, lw=3, ls='dotted', label=label)
        label = ''
        cxy = [p[0], p[1] + (f_wb_p-p[1])/2]
        ax.annotate(f'{c_p_txt:0.0f}', xy=cxy, xycoords='data',
                    xytext=(5, 0), textcoords='offset points')


def plt_stationary(x_train, y_train, w0, b):
    fig, ax = plt.subplots(1, 2, figsize=(9, 8))
    fig.canvas.toolbar_position = 'top'

    w_range = np.array([200-300., 200+300])
    b_range = np.array([50-300., 50+300])
    b_space = np.linspace(*b_range, 100)
    w_space = np.linspace(*w_range, 100)

    tmp_b, tmp_w = np.meshgrid(b_space, w_space)
    z = np.zeros_like(tmp_b)
    for i in range(tmp_w.shape[0]):
        for j in range(tmp_w.shape[1]):
            z[i, j] = cost_fxn(x_train, y_train, tmp_w[i][j], tmp_b[i][j])
            if z[i, j] == 0:
                z[i, j] = 1e-6

    f_wb = np.dot(x_train, w0) + b
    mk_cost_lines(x_train, y_train, w0, b, ax[0])
    plt_house_x(x_train, y_train, f_wb=f_wb, ax=ax[0])

    CS = ax[1].contour(tmp_w, tmp_b, np.log(z), levels=12,
                       linewidths=2, alpha=0.7)
    ax[1].set_title('Cost(w,b) [Contour Plot]')
    ax[1].set_xlabel('w', fontsize=10)
    ax[1].set_ylabel('b', fontsize=10)
    ax[1].set_xlim(w_range)
    ax[1].set_ylim(b_range)
    cscat = ax[1].scatter(w0, b, s=100, zorder=10,)
    chline = ax[1].hlines(b, ax[1].get_xlim()[0], w0,
                          lw=4, ls='dotted')
    cvline = ax[1].vlines(w0, ax[1].get_ylim()[0], b,
                          lw=4, ls='dotted')
    fig.tight_layout()
    return fig, ax, [cscat, chline, cvline]


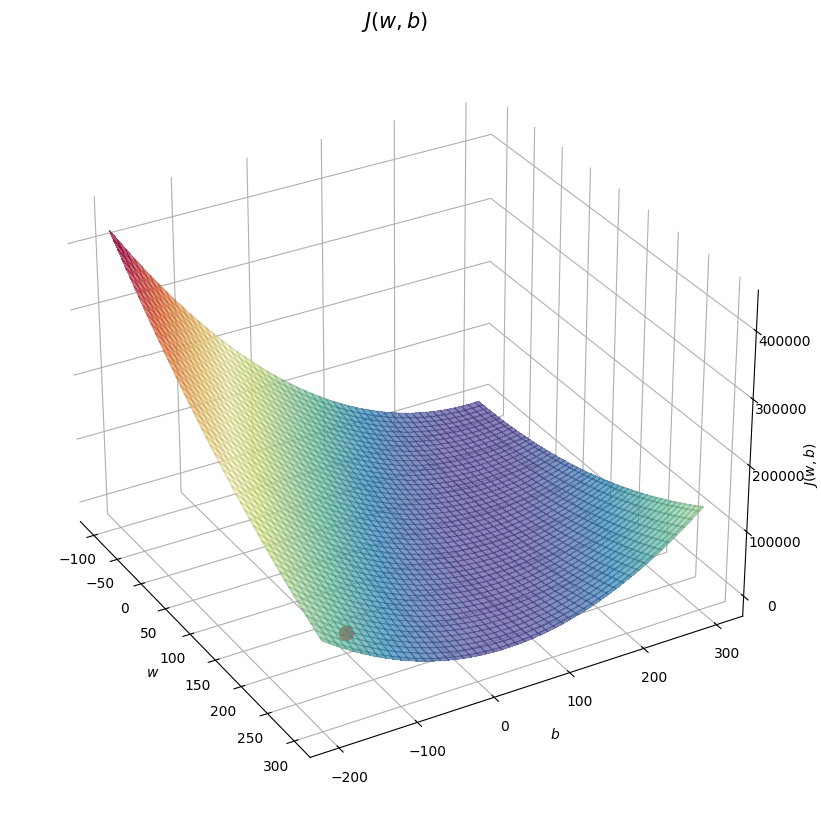
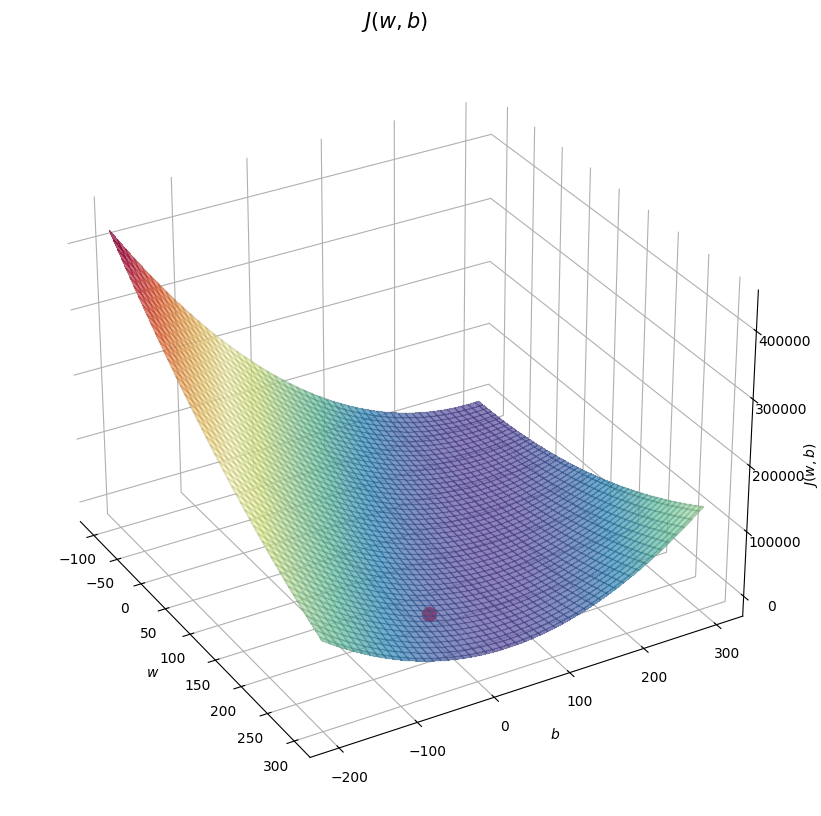
def soup_bowl(x_train, y_train, w0=200, b0=-100):
    fig = plt.figure(figsize=(10, 10))

    ax = fig.add_subplot(111, projection='3d')
    ax.xaxis.set_pane_color((1.0, 1.0, 1.0, 0.0))
    ax.yaxis.set_pane_color((1.0, 1.0, 1.0, 0.0))
    ax.zaxis.set_pane_color((1.0, 1.0, 1.0, 0.0))
    ax.zaxis.set_rotate_label(False)
    ax.view_init(30, -30)

    w = np.linspace(-100, 300, 100)
    b = np.linspace(-200, 300, 100)

    z = np.zeros((len(w), len(b)))
    for i in range(len(w)):
        for j in range(len(b)):
            z[i, j] = cost_fxn(x_train, y_train, w[i], b[j])

    W, B = np.meshgrid(w, b)

    ax.plot_surface(W, B, z, cmap="Spectral_r", alpha=0.7, antialiased=False)
    ax.plot_wireframe(W, B, z, color='k', alpha=0.1)
    ax.set_xlabel("$w$")
    ax.set_ylabel("$b$")
    ax.set_zlabel("$J(w,b)$", rotation=90)
    ax.set_title("$J(w,b)$", size=15)
    cscat = ax.scatter(w0, b0, s=100, color='red')

    plt.show()

Dataset

x_train = np.array([1.0, 1.7, 2.0, 2.5, 3.0, 3.2])
y_train = np.array([250, 300, 480, 430, 630, 730])
w = 200
b = -100

Finding Function f_wb

\[ f_{w,b}(x^{(i)}) = wx^{(i)} + b \]

def fxn(x, w, b):
    f_wb = w * x + b

    return f_wb

Finding Cost Function

\[J(w,b) = \frac{1}{2m} \sum\limits_{i = 0}^{m-1} (f_{w,b}(x^{(i)}) - y^{(i)})^2\]

def cost_fxn(x, y, w, b):
    m = x.shape[0]

    f_wb = fxn(x, w, b)
    cost = (f_wb - y) ** 2
    total_cost = (1 / (2 * m)) * np.sum(cost)

    return total_cost

Some Plots ->

Original w, b

fig, ax, dyn_items = plt_stationary(x_train, y_train, w, b)
soup_bowl(x_train, y_train, w, b)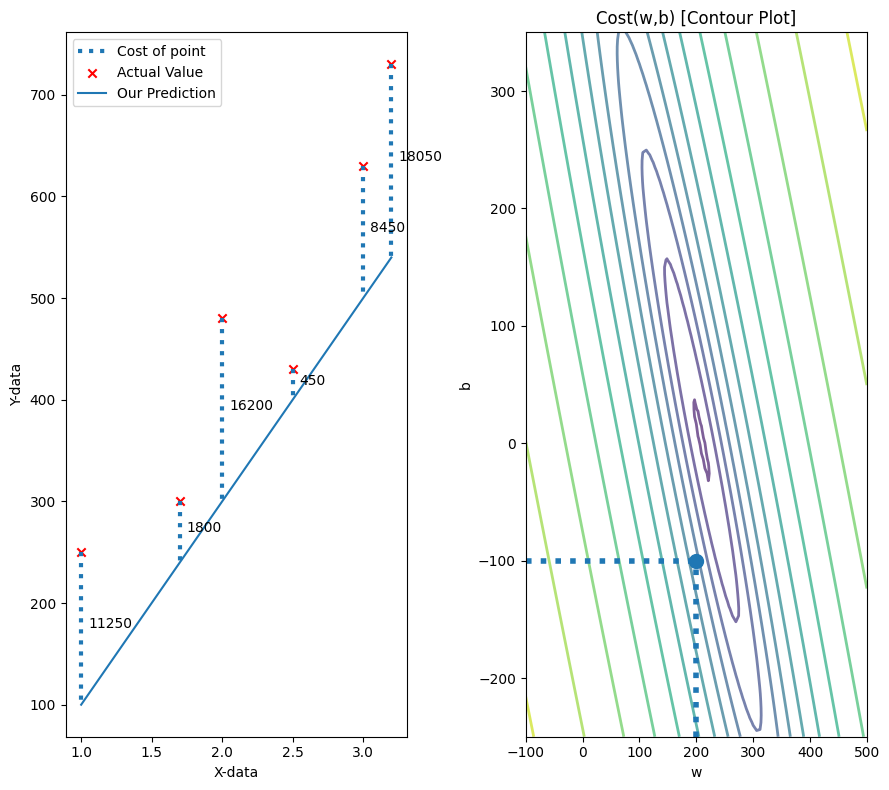

Finding dJ/dw and dJ/db

\[ \frac{\partial J(w,b)}{\partial w} = \frac{1}{m} \sum\limits_{i = 0}^{m-1} (f_{w,b}(x^{(i)}) - y^{(i)})x^{(i)} \\ \frac{\partial J(w,b)}{\partial b} = \frac{1}{m} \sum\limits_{i = 0}^{m-1} (f_{w,b}(x^{(i)}) - y^{(i)}) \\ \]

def compute_gradient(x, y, w, b):
    m = x.shape[0]
    a = fxn(x, w, b) - y
    dj_dw = (np.dot(a, x))/m
    dj_db = np.sum(a)/m
    return dj_dw, dj_db

Gradient Descent

\[\begin{align*} \text{repeat}&\text{ until convergence:} \; \lbrace \newline \; w &= w - \alpha \frac{\partial J(w,b)}{\partial w} \; \newline b &= b - \alpha \frac{\partial J(w,b)}{\partial b} \newline \rbrace \end{align*}\] where, parameters \(w\), \(b\) are updated simultaneously.

def gradient_descent(x, y, w, b, alpha, num_iters):
    J_history = []
    p_history = []

    for i in range(num_iters + 1):
        dj_dw, dj_db = compute_gradient(x, y, w, b)
        w -= alpha * dj_dw
        b -= alpha * dj_db

        cost = cost_fxn(x, y, w, b)
        J_history.append(cost)
        p_history.append((w, b))

        if i % math.ceil(num_iters / 10) == 0:
            print(f"Iteration {i:4}: Cost {cost:.2e}, w: {w}, b: {b}")

    return w, b, J_history, p_history


iterations = 10000
tmp_alpha = 1.0e-2

w_final, b_final, J_hist, p_hist = gradient_descent(
    x_train, y_train, w, b, tmp_alpha, iterations)
print(f"(w,b) found by gradient descent: {w_final},{b_final}")


f_wb = fxn(x_train, w_final, b_final)
print("Cost is", cost_fxn(x_train, y_train, w_final, b_final))

fig, ax = plt.subplots(figsize=(6, 4))
ax.plot(1000 + np.arange(len(J_hist[1000:])), J_hist[1000:])
ax.set_title("Cost vs. iteration (end)")
ax.set_ylabel('Cost')
ax.set_xlabel('iteration step')
plt.show()

Iteration    0: Cost 8.46e+03, w: 202.80833333333334, b: -98.76666666666667
Iteration 1000: Cost 1.80e+03, w: 223.52137552092964, b: -32.28296188836681
Iteration 2000: Cost 1.75e+03, w: 215.18089273879156, b: -11.838434218472974
Iteration 3000: Cost 1.74e+03, w: 211.75363820423198, b: -3.4374097221896087
Iteration 4000: Cost 1.74e+03, w: 210.3453176127893, b: 0.014722492685807966
Iteration 5000: Cost 1.74e+03, w: 209.76661332681294, b: 1.4332657708600276
Iteration 6000: Cost 1.74e+03, w: 209.5288133168987, b: 2.0161707428604965
Iteration 7000: Cost 1.74e+03, w: 209.43109701154987, b: 2.255696890289678
Iteration 8000: Cost 1.74e+03, w: 209.39094362242898, b: 2.3541224966202314
Iteration 9000: Cost 1.74e+03, w: 209.37444387193037, b: 2.394567350284724
Iteration 10000: Cost 1.74e+03, w: 209.3676638273943, b: 2.4111868688115714
(w,b) found by gradient descent: 209.3676638273943,2.4111868688115714
Cost is 1735.8832116012204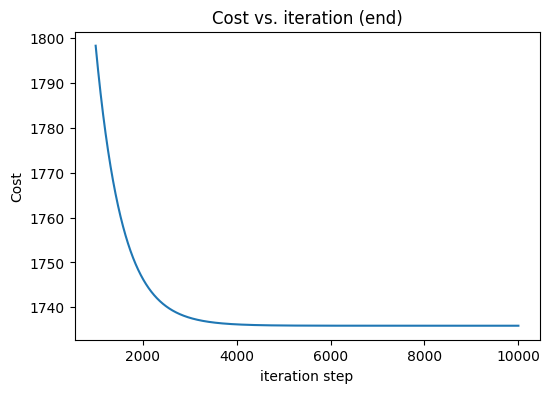

Some Plots ->

Final w, b

fig, ax, dyn_items = plt_stationary(x_train, y_train, w_final, b_final)
soup_bowl(x_train, y_train, w_final, b_final)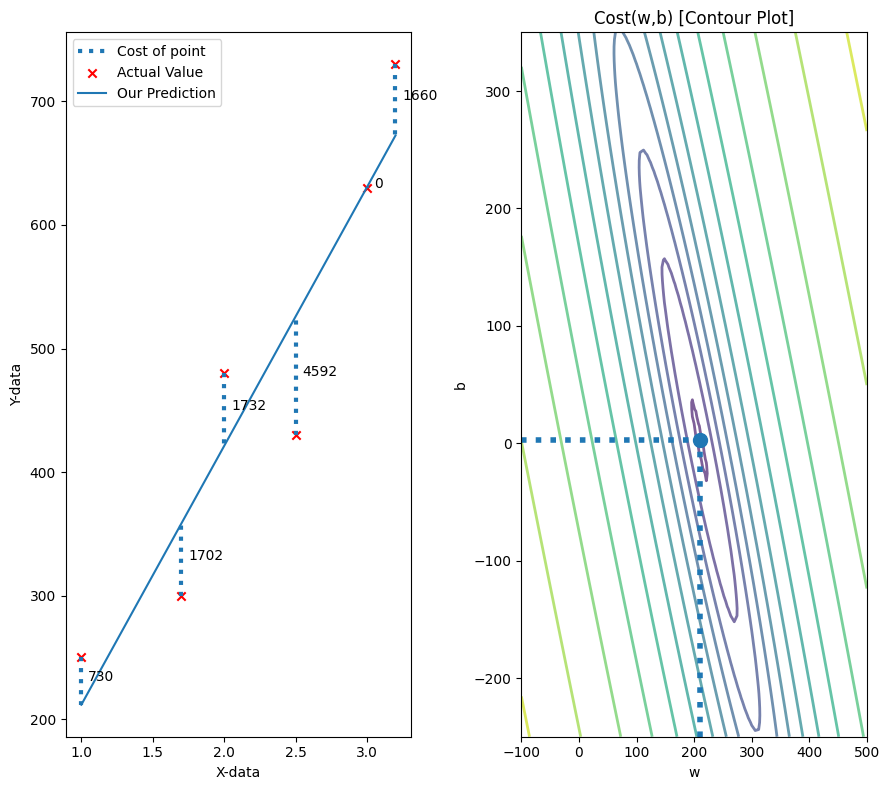

Regularized Linear Regression

Finding Cost Fxn

\[J(\mathbf{w},b) = \frac{1}{2m} \sum\limits_{i = 0}^{m-1} (f_{\mathbf{w},b}(\mathbf{x}^{(i)}) - y^{(i)})^2 + \frac{\lambda}{2m} \sum_{j=0}^{n-1} w_j^2 \]

def cost_fxn_regularized(X, y, w, b, lambda_=1):
    cost = cost_fxn(X, y, w, b)
    cost += np.sum(w ** 2)
    return cost

Finding dJ/dw and dJ/db

\[\begin{align*} \frac{\partial J(\mathbf{w},b)}{\partial w_j} &= \frac{1}{m} \sum\limits_{i = 0}^{m-1} (f_{\mathbf{w},b}(\mathbf{x}^{(i)}) - y^{(i)})x_{j}^{(i)} + \frac{\lambda}{m} w_j \\ \frac{\partial J(\mathbf{w},b)}{\partial b} &= \frac{1}{m} \sum\limits_{i = 0}^{m-1} (f_{\mathbf{w},b}(\mathbf{x}^{(i)}) - y^{(i)}) \end{align*}\]

def compute_gradient_regularized(X, y, w, b, lambda_):
    m = X.shape[0]
    dj_dw, dj_db = compute_gradient(X, y, w, b)

    dj_dw += (lambda_ / m) * w

    return dj_db, dj_dw